Wie funktioniert Machine Learning?
Künstliche Intelligenz (KI) und Machine Learning (ML) sind gefühlt allgegenwärtig und werden in den nächsten Jahren immer wichtiger werden. Typische Anwendungsbeispiele für ML sind personalisierte Vorschläge von Streaming-Diensten, Assistenzsysteme im Auto und Sprachassistenten. Viele Menschen nutzen KI-Systeme bewusst oder auch unbewusst, aber die wenigsten wissen, was im Hintergrund passiert. Dieser Artikel zeigt mit einfachen Beispielen, wie Machine Learning funktioniert. Dazu wird in leicht nachvollziehbaren Schritten ein einfaches ML-Modell mit Python und der beliebten Bibliothek scikit-learn erstellt und angewendet. Dabei werden ganz nebenbei einige wichtige ML-Begriffe eingeführt und erklärt.
Viele der folgenden Aussagen sind verallgemeinert und vereinfacht. Weiterhin gibt es zum vorgestellten Ablauf oft Alternativen, Ausnahmen und Abweichungen. Um den Artikel nicht unnötig aufzublähen und den Lesefluss nicht kontinuierlich zu stören, wird das ganz bewusst in Kauf genommen.
Der gezeigte Python-Code wurde genutzt, um die Ausgaben und Diagramme zu erstellen. Für das Verständnis des Artikels ist der Code nicht notwendig und er kann beim Lesen übersprungen werden.
Daten analysieren
Beim Maschinellen Lernen werden existierende Daten verwendet, um damit einen Algorithmus, hier wird auch von einem Modell gesprochen, zu trainieren. Dieses Modell wird dann verwendet, um mit neuen Daten eine Vorhersage zu treffen.
Abstrakt formuliert wird beim Trainieren eines Modells eine mathematische Funktion gesucht, die anhand existierender Daten in der Lage ist, das erwartete Ergebnis möglichst genau vorherzusagen. Solch eine Funktion (bzw. Modell) sollte dann auch mit neuen, bisher unbekannten Daten eine korrekte Ausgabe (Vorhersage) liefern.
In der Praxis stellt sich die Beschaffung geeigneter Daten oft als schwierig und zeitaufwändig heraus. Für diesen Artikel werden Beispieldaten, die in scikit-learn enthalten sind, verwendet. Diese Daten werden auch Dataset genannt.
Iris Flower Dataset
Dieses Dataset enthält die folgenden Daten:
- 50 Samples (Datensätze) von drei unterschiedlichen Arten der Schwertlilie:
- setosa (Borsten-Schwertlilie)
- versicolor (Verschiedenfarbige Schwertlilie)
- virginica (Virginische Schwertlilie)
- 150 Samples (Datensätze) insgesamt
- Die Datensätze haben diese Attribute:
- sepal length (Länge des Kelchblattes)
- sepal width (Breite des Kelchblattes)
- petal length (Länge des Kronblattes)
- petal width (Breite des Kronblattes)
- class (setosa, versicolor oder virginica)
from IPython.display import Image Image(filename="iris.png")
Daten laden
Zuerst werden die Daten in den Hauptspeicher geladen. Im Beispiel wird die Funktion sklearn.datasets.load_iris verwendet. Anschließend wird die Beschreibung des Datasets ausgegeben.
Das Paket scikit-learn.datasets enthält noch weitere Funktionen zum Laden und Generieren von unterschiedlichen Datasets. Diese werden in der Dokumentation ausführlich beschrieben.
https://scikit-learn.org/stable/datasets.html
from sklearn import datasets # Laden der Daten iris = datasets.load_iris() # Ausgabe der Beschreibung print(iris.DESCR)
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
.. topic:: References
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
Features & Target
Im Iris Dataset wird intern zwischen Feature und Target unterschieden.
Ein Feature ist ein Merkmal bzw. ein Attribut eines Datensatzes. Features sind üblicherweise Eingabedaten anhand derer ein Ergebnis vorhergesagt werden soll. Die einzelnen Datensätze werden mathematisch als Vektor betrachtet und oft als Feature Vector bezeichnet.
Als Target wird das erwartete Ergebnis bezeichnet. Im Iris Dataset ist die Art (class) der Schwertlilie als Target enthalten. Eine andere Bezeichnung für Target ist auch Label.
Mit dem folgenden Code werden die Daten des Iris Datasets ausgegeben.
# Ausgabe der Namen der einzelnen Spalten (Features)
print('Feature Names:')
print(iris.feature_names)
# Ausgabe der Daten
print('Feature Data:')
print(iris.data)
Feature Names:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
Feature Data:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
...
[5.9 3. 5.1 1.8]]
# Ausgabe der verschiedenen Arten von Schwertlilien
print('Target Names:')
print(iris.target_names)
# Ausgabe der numerischen Werte (Label) für die Arten
print('Target Values:')
print(iris.target)
Target Names:
['setosa' 'versicolor' 'virginica']
Target Values:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Pandas DataFrame
Für die weitere Analyse wird mit den Daten ein Pandas DataFrame erzeugt.
Pandas ist eine Bibliothek, die Datenstrukturen und Analysefunktionen für Python bereitstellt. Etwas vereinfacht ist ein Pandas DataFrame eine Tabelle mit Spalten und Datentypen. Über leistungsfähige Funktionen können die Daten in einem DataFrame sehr leicht analysiert und modifiziert werden. Man kann sich ein Pandas DataFrame auch als Excel-Tabelle vorstellen, die mit Python statt mit Maus und Tastatur bedient wird.
Eine ausführliche Beschreibung gibt es auf der Homepage des Projektes:
https://pandas.pydata.org/pandas-docs/stable/index.html
Im erzeugten DataFrame wird nicht mehr explizit zwischen Feature und Target unterschieden. Die Daten mit der Art werden in die zusätzliche Spalte class eingefügt. Der Grund ist einfach: Für die folgenden Beispiele soll nicht die Art, sondern ein anderes Attribut vorhergesagt werden.
import pandas as pd # Neues DataFrame mit den Iris-Daten (Features) erzeugen iris_df = pd.DataFrame(iris.data, columns = iris.feature_names) # Neue Spalte class (Target) zum DataFrame hinzufügen iris_df['class'] = iris.target # DataFrame ausgeben iris_df
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | class | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
150 rows × 5 columns
DataFrame Info
Mit der Funktion info() werden allgemeine Informationen ausgegeben. Neben dem Schema (Spalten und Datentypen) sind das zum Beispiel die Anzahl der Datensätze und der belegte Speicherplatz.
# Weitere Informationen zum DataFrame ausgeben iris_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal length (cm) 150 non-null float64
1 sepal width (cm) 150 non-null float64
2 petal length (cm) 150 non-null float64
3 petal width (cm) 150 non-null float64
4 class 150 non-null int64
dtypes: float64(4), int64(1)
memory usage: 6.0 KB
DataFrame Describe
Die Funktion describe() liefert einige wichtige statistische Kennzahlen zu den einzelnen Spalten im DataFrame.
# Statistische Kennzahlen ausgeben iris_df.describe()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | class | |
|---|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.057333 | 3.758000 | 1.199333 | 1.000000 |
| std | 0.828066 | 0.435866 | 1.765298 | 0.762238 | 0.819232 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 | 0.000000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 | 0.000000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 | 1.000000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 | 2.000000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 | 2.000000 |
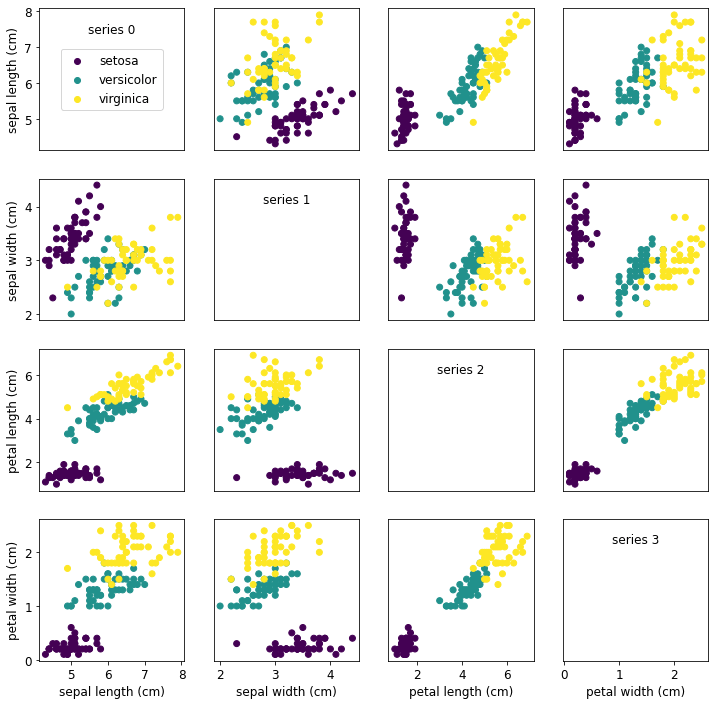
Scatterplot Matrix
Als nächstes wird eine Scatterplot-Matrix erstellt. Dazu werden in zweidimensionalen Diagrammen immer zwei Attribute aus den Daten auf der x- und y-Achse aufgetragen. Im Fall der Iris-Daten wird das für die verschiedenen Längenangaben gemacht. Die Art (class) wird als Farbe der Punkte dargestellt.
Eine Scatterplot-Matrix ist gut geeignet, um Zusammenhänge zwischen den verschiedenen Attributen visuell darzustellen. Das funktioniert allerdings nur bei einer noch überschaubaren Anzahl an Attributen (Features).
Für die Plots wird die Bibliothek matplotlib verwendet. Eine ausführliche Dokumentation und viele Tutorials gibt es auf der Homepage des Projektes:
https://matplotlib.org/
# Anzahl der Features, Datensätze (Vektoren) und die unterschiedlichen Arten (class) ermitteln
# Die letzte Spalte (class) wird im Scatterplot nicht dargestellt
num_features = iris_df.shape[1]-1
num_vectors = iris_df.shape[0]
num_classes=iris_df['class'].max() + 1
class_names = iris.target_names
print("num_features: {:>3}".format(num_features))
print("num_vectors : {:>3}".format(num_vectors))
print("num_classes : {:>3}".format(num_classes))
print("class_names : {}".format(class_names))
num_features: 4
num_vectors : 150
num_classes : 3
class_names : ['setosa' 'versicolor' 'virginica']
import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import cm
# Colormap mit einer Farbe für jede Art (class) definieren
cmap_iris = cm.get_cmap('viridis', num_classes)
# Standard Schriftgröße setzen
mpl.rcParams['font.size'] = 12.0
# Erzeuge für jede Kombination von Featuren einen eigenen Plot
# d.h. 4 * 4 Plots
fig, ax = plt.subplots(num_features, num_features, figsize=(12,12))
# Das Feature 'class' wird für alle Plots als Farbe verwendet
c = iris_df.iloc[:, 4]
for i in range(num_features):
for j in range(num_features):
# Plotte Spalte j auf x-Achse und Spalte i auf y-Achse
if i != j:
x = iris_df.iloc[: ,j]
y = iris_df.iloc[:, i]
ax[i][j].scatter(x, y, c=c, cmap=cmap_iris)
# Außer wenn i == j
# dann wird ein Text mit dem Index des Features / der Spalte ausgegeben
else: ax[i][j].annotate("series " + str(i), (0.5, 0.9),
xycoords='axes fraction',
ha="center", va="top")
# Setze Label für x- und y-Achse
ax[i][j].set_xlabel(iris_df.columns[j])
ax[i][j].set_ylabel(iris_df.columns[i])
# Verstecke Label außer für linke Spalte und unterste Zeile in der Matrix
if i < num_features - 1: ax[i][j].xaxis.set_visible(False)
if j > 0: ax[i][j].yaxis.set_visible(False)
# Legende im oberen linken Plot erzeugen
for c in range(num_classes):
ax[0][0].scatter([0], [0], color=cmap_iris(c), label=class_names[c])
ax[0][0].legend(loc='center')
# Korrigiere Achsen Limits für obersten-linken und untersten-rechten Plot
ax[-1][-1].set_xlim(ax[0][-1].get_xlim())
ax[0][0].set_ylim(ax[0][1].get_ylim())
plt.show()
Analyse
Die verschiedenen Plots zeigen deutlich, dass es einen Zusammenhang (Korrelation) zwischen den verschiedenen Werten der Schwertlilie und der Art gibt.
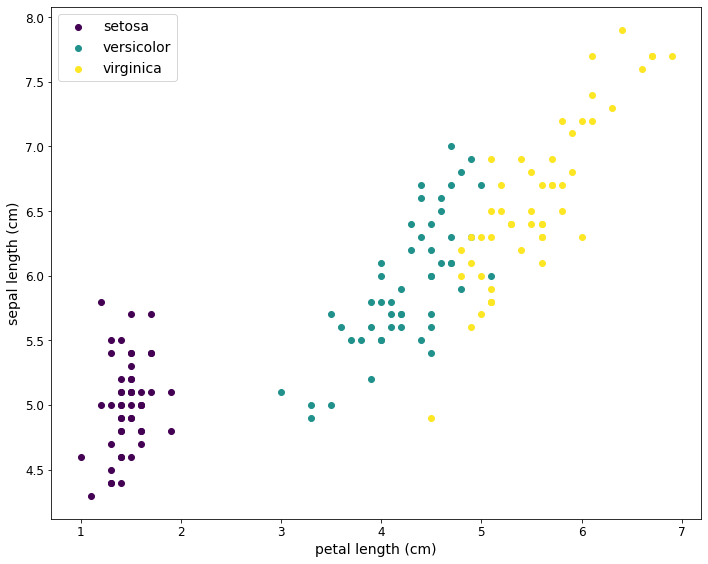
Für das erste Modell wird nicht die Art der Schwertlilie bestimmt. Stattdessen soll anhand der Länge des Kronblattes (petal length) die Länge des Kelchblattes (sepal length) vorhergesagt werden.
Zuerst wird das entsprechende Diagramm nochmals etwas größer ausgegeben.
# x-Achse # petal length x_index = 2 x_label=iris_df.columns[x_index] # y-Achse # sepal length y_index= 0 y_label=iris_df.columns[y_index]
# Funktion zum Erzeugen eines 2-D-Diagramms
def scatter_plot_2d(legend=True, figsize=(10, 8)):
c_col = 'class'
colors = cmap_iris
labels = class_names
fig, axes = plt.subplots(figsize=figsize)
# Erzeuge eine Gruppe für jede Art
groups = iris_df.groupby('class')
# Erzeuge einen eigenen Plot für jede Gruppe
# Dadurch kann eine Legende für die einzelnen Arten angezeigt werden
for name, group in groups:
axes.scatter(group[x_label], group[y_label], label=class_names[name], color=cmap_iris(name))
fontsize = 14
axes.set_xlabel(x_label, fontsize=fontsize)
axes.set_ylabel(y_label, fontsize=fontsize)
plt.tight_layout()
# Anzeige der Legende
if legend: axes.legend(fontsize=fontsize)
return fig, axes
# Diagramm erzeugen und anzeigen fig, axes = scatter_plot_2d()
Einfaches Modell erstellen
Im nächsten Schritt wird mit den Daten ein Modell erstellt und trainiert. Für dieses Beispiel wird als Algorithmus die Lineare Regression verwendet. Wie bereits erwähnt, soll aus dem Wert des Features petal length der Wert für sepal length vorhergesagt werden. Bei der Linearen Regression wird eine lineare Funktion verwendet, mit der für einen beliebigen Feature-Vektor x der Wert y vorhergesagt (predict) wird.
f(x) = wx + b
In diesem Bespiel wird bewusst nur ein Feature verwendet. Die Funktion liefert als Ergebnis eine einfache Gerade.
w ist die Steigung
b ist der Schnittpunkt mit der y-Achse
Um eine erste Vorhersage zu treffen, können Werte für w und b in diesem Fall visuell anhand des Diagramms ermittelt bzw. geschätzt werden. Für den ersten Versuch werden die folgenden Werte verwendet:
w = 0.5
b = 4.5
f(x) = 0.5x + 4.5
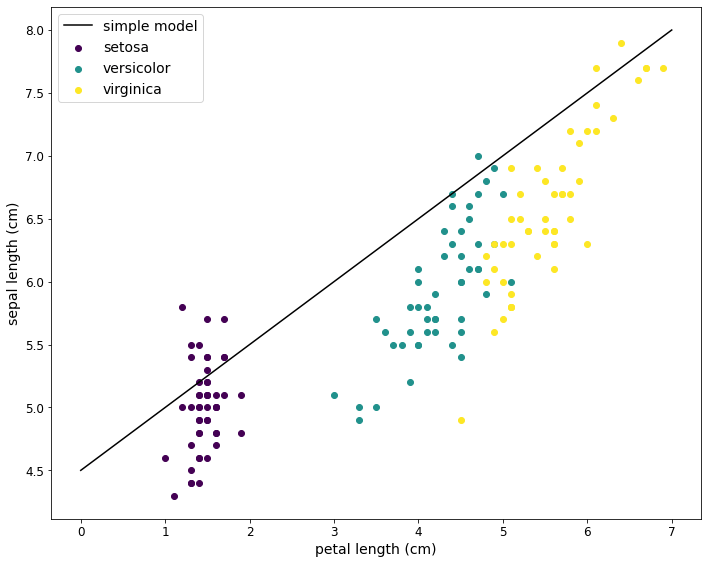
Mit diesen Werten wird ein einfaches Modell (eine Funktion) erstellt. Das Ergebnis dieses Modells wird dann im Diagramm eingezeichnet.
# Einfaches Modell mit geschätzten Werten für w und b
def simple_model(x):
y = 0.5 * x + 4.5
return y
import numpy as np # Diagramm erstellen # - Features (setosa, versicolor, virginica) # - Vorhersage der Funktion (simple model) fig, axes = scatter_plot_2d(False) # Das einfache Modell berechnet Vorhersagen für die Werte 0 und 7 R = np.array([0,7]) axes.plot(R, simple_model(R.reshape(-1,1)),color='k', label='simple model') axes.legend(fontsize=14) plt.show()
Machine Learning
Für den Anfang war das Schätzen der Werte für w und b nicht schlecht. Mit etwas Trial and Error wäre es für diesen einfachen Fall möglich, die optimalen Parameter zu finden. In der Realität ist das üblicherweise nicht so einfach, da die Zusammenhänge meist deutlich komplexer sind.
Statt die Werte durch manuelles Ausprobieren zu ermitteln, können die optimalen Parameter mit mathematischen Verfahren automatisch ermittelt werden.
Dazu wird eine sogenannte Loss Function ausgewählt. Mit dieser wird der Fehler der Vorhersage berechnet. Ziel ist es, dass der Fehler möglichst gering ist und die Gerade die Daten somit möglichst gut abbildet. Die im Folgenden verwendete Funktion wird Squared Error Loss genannt.
1/N ∑Ni=1(f(xi)−yi)2
Beim Training des Modells wird für alle Trainingsdaten (x1,x2,...,xN) die Differenz zwischen dem vorhergesagten Wert der Funktion f(x) und dem bekannten Wert (Label) (y1,y2,...,yN) aus den Trainingsdaten ermittelt. Diese Differenz entspricht dem Abstand zwischen der Geraden (Prediction) und dem erwarteten Wert (Label).
Die Quadrate dieser Differenzen werden aufsummiert und durch die Anzahl der Datensätze in den Trainingsdaten geteilt. Die Parameter w und b werden beim Training so lange variiert, bis die Loss Function den minimalen Wert liefert.
Die verschiedenen Verfahren und Funktionen zum Trainieren eines Modells müssen nicht selbst programmiert werden. Stattdessen können fertige Bibliotheken, wie zum Beispiel scikit-learn, eingesetzt werden.
Trainings- und Testdaten
Um ein Modell zu trainieren, werden die vorhandenen Daten zuerst in Trainingsdaten und Testdaten aufgeteilt.
Diese Trennung ist wichtig, denn das Modell soll später mit unbekannten/neuen Daten gute Ergebnisse liefern. Wenn das Modell mit allen bekannten Daten trainiert wird, dann gibt es im Vorfeld keine Möglichkeit zu prüfen, wie gut die Vorhersagen für neue Daten sein werden. Die Trainingsdaten werden zum Trainieren des Modells verwendet. Anhand dieser Daten werden die optimalen Parameter ermittelt. Die Testdaten sind neue/unbekannte Daten und werden verwendet, um die Genauigkeit bzw. die Qualität des fertig trainierten Modells zu berechnen.
Im folgenden Beispiel wird diese Trennung mit der Funktion model_selection.train_test_split() durchgeführt. Der weitere Code wird benötigt, um die Daten in das richtige Format für scikit-learn zu bringen.
from sklearn import model_selection # 30 % der Daten werden als Testdaten reserviert test_size = 0.30 # Testdaten werden zufällig ausgewählt # Damit bei jeder Ausführung des Codes immer die gleichen Daten verwendet werden, # muss der Zufallszahlengenerator mit einer Konstanten initialisiert werden # Auf die Frage, welcher Wert hier verwendet werden soll, ist 42 natürlich die richtige Antwort;) random_state = 42 # x-Achste # petal length x_index = 2 X1 = iris_df.iloc[: ,x_index].to_numpy() # y-Achse # sepal length y_index = 0 Y1 = iris_df.iloc[:, y_index].to_numpy() # Aufteilen in Trainings und Testdaten X1_train, X1_test, Y1_train, Y1_test = model_selection.train_test_split(X1, Y1, test_size=test_size, random_state=random_state) # Das Modell erwartet ein 2-dimensionales Array (eine Matrix) # Die Funktion reshape erstellt aus einem eindimensionalen Array ein 2-dimensionales Array (eine Matrix) X1_train = X1_train.reshape(-1, 1) Y1_train = Y1_train.reshape(-1, 1) X1_test = X1_test.reshape(-1, 1) Y1_test = Y1_test.reshape(-1, 1)
Trainieren des Modells
Als nächstes wird ein LinearRegression-Modell erstellt und trainiert. Die Funktion fit() erwartet als Eingabe die Features (X1_train) und das erwartete Ergebnis bzw. die Labels (Y1_train).
from sklearn import linear_model # Modell erstellen model1 = linear_model.LinearRegression() # Modell trainieren model1.fit(X1_train, Y1_train)
LinearRegression()
Modell validieren
Als letzter Schritt wird noch die Qualität des Modells überprüft. In diesem Fall wird dazu mit den Testdaten die Accuracy (Genauigkeit) berechnet. Die Genauigkeit ist der Prozentsatz der Vorhersagen, die richtig sind.
# Accuracy berechnen und ausgeben
score1 = model1.score(X1_test, Y1_test)
print("Accuracy: %.2f%% (1 Feature, LinearRegression)" % (score1 * 100.0))
Accuracy: 76.74% (1 Feature, LinearRegression)
Das Modell kann somit in 76.74% der Fälle das richtige Egebnis vorhersagen. Umgekehrt sind aber 23,26% der Vorhersagen falsch.
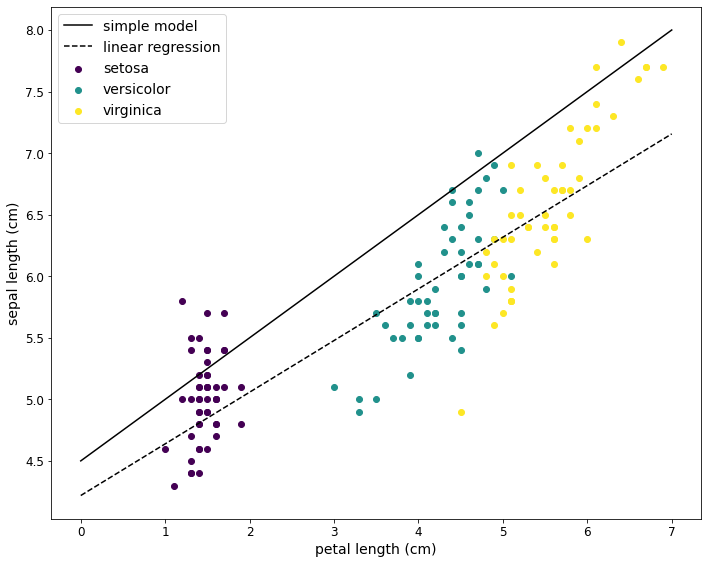
Vorhersage plotten
Das Ergebnis der Vorhersage kann auch als Diagramm dargestellt werden. Die durchgezogene Linie ist die Vorhersage des Modells mit den geschätzten Parametern. Die gestrichelte Linie ist die Vorhersage des LinearRegression-Modells.
# Diagramm erstellen # - Features (setosa, versicolor, virginica) # - Vorhersage der einfachen Funktion (simple model) # - Vorhersage des LinearRegression-Modells fig, axes = scatter_plot_2d(False) R = np.array([0,7]) plt.plot(R, simple_model(R.reshape(-1,1)), color = 'k', label = "simple model") plt.plot(R, model1.predict(R.reshape(-1,1)), color = 'k', linestyle = "--" , label="linear regression") axes.legend(fontsize=14) plt.show()
Wie man sieht, ist das ML-Modell besser als das manuell erstellte Modell.
Ist das alles?
Nein, das war erst der Anfang.
Mehr Features
In der Realität werden üblicherweise mehr Features (Attribute) zum Trainieren verwendet. Ein einzelner Datensatz mit mehreren Featuren wird als Vektor betrachtet und die Menge der Datensätze als Matrix. Auch das Ergebnis (Vorhersage) des Modells kann aus mehreren Attributen und somit aus einem Vektor bestehen.
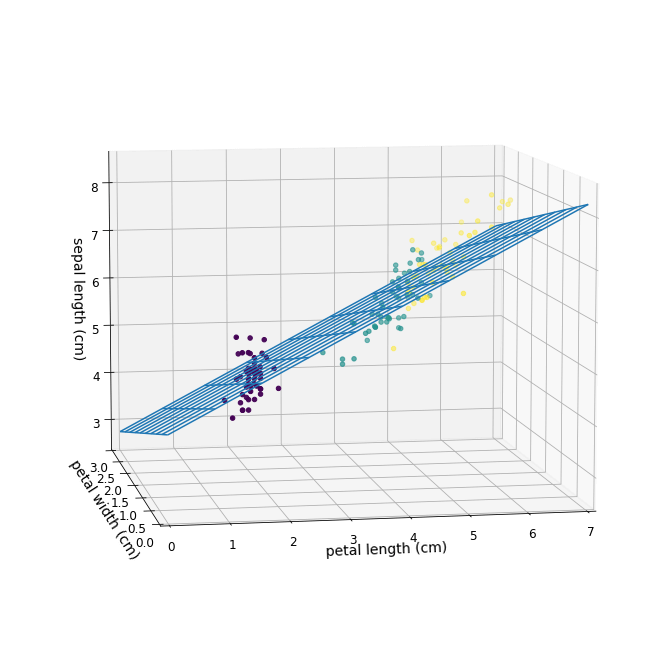
Die Modelle (Funktionen) werden dann mit den Daten in einer Feature-Matrix X trainiert. Für zwei Features kann das in einem dreidimensionalen Diagramm visualisiert werden. Bei mehr als drei Features ist das dann nicht mehr möglich.
Das folgende Beispiel zeigt ein Modell, bei dem die beiden Features petal length (Länge des Kronblattes) und petal width (Breite des Kronblattes) für die Vorhersage der sepal length (Länge des Kelchblattes) verwendet werden.
# x-Achse
# petal length
x2_index = 2
x2_label=iris_df.columns[x2_index]
# y-Achse
y2_index= 3
y2_label=iris_df.columns[y2_index]
# z-Achse
# sepal length
z2_index= 0
z2_label=iris_df.columns[z2_index]
# petal length in cm
# petal width in cm
X2 = iris.data[:, [x2_index,y2_index]]
# sepal length in cm
Y2 = Y1
# Trennen von Trainings- und Testdaten
X2_train, X2_test, Y2_train, Y2_test = model_selection.train_test_split(X2, Y2, test_size=test_size, random_state=random_state)
Y2_train = Y2_train.reshape(-1, 1)
Y2_test = Y2_test.reshape(-1, 1)
# Modell erstellen und trainieren
model2 = linear_model.LinearRegression()
model2.fit(X2_train, Y2_train)
# Genauigkeit berechnen und ausgeben
score2 = model2.score(X2_test, Y2_test)
print("Accuracy: %.2f%% (2 Features, LinearRegression)" % (score2 * 100.0))
Accuracy: 75.54% (2 Features, LinearRegression)
Die Genauigkeit (Accuracy) ist in diesem Fall schlechter als beim ersten Beispiel, in dem nur ein Feature verwendet wurde. Solche Effekte sind nicht unüblich. Die optimalen Features zu ermitteln ist eine Kunst. Die Aufbereitung der Rohdaten und die Auswahl der Features sind wichtige Aspekte des sogenannten Feature Engineerings. In der Praxis gehört das Feature Engineering oft zu den aufwändigsten Tätigkeiten beim Trainieren eines Modells.
Im folgenden 3D-Diagramm werden die verwendeten Daten wieder als Punkte angezeigt und die Vorhersage des Modells wird als zusätzliche Ebene dargestellt.
# 3-D-Diagramm der Daten erstellen from mpl_toolkits.mplot3d import Axes3D X1 = iris_df.iloc[: ,x_index].to_numpy() x2_data=iris_df.iloc[: ,x2_index] y2_data=iris_df.iloc[: ,y2_index] z2_data=iris_df.iloc[: ,z2_index] C=iris.target fig = plt.figure(figsize=(12, 12)) ax = fig.add_subplot(111, projection='3d') ax.scatter3D(x2_data, y2_data, z2_data, c=C, cmap=cmap_iris) fontsize=14 ax.set_xlabel(x2_label, fontsize = fontsize) ax.set_ylabel(y2_label, fontsize = fontsize) ax.set_zlabel(z2_label, fontsize = fontsize) # Ebene mit Vorhersagen hinzufügen num = 10 XM = np.linspace(0, 7, num) YM = np.linspace(0, 3, num) XM, YM = np.meshgrid(XM, YM) ZM = model2.predict(np.c_[XM.ravel(), YM.ravel()]) ZM = ZM.reshape(num,num) ax.plot_wireframe(XM, YM, ZM) ax.set_xlim(0, 7) ax.set_ylim(0, 3) # Diagramm anzeigen ax.view_init(8, 260)
Linear Regression Variationen
Es gibt Variationen für die Lineare Regression. Zum Beispiel können Polynome genutzt werden, um nicht-lineare Verläufe vorherzusagen.
Im folgenden Beispiel wird ein Polynom 6. Grades verwendet, um ein LinearRegression-Modell zu trainieren.
from sklearn import preprocessing
# Die Features werden mit einem Polynom transformiert
degree=6
polynomial_features = preprocessing.PolynomialFeatures(degree = degree)
X3_train = polynomial_features.fit_transform(X1_train)
Y3_train = Y1_train
X3_test = polynomial_features.fit_transform(X1_test)
Y3_test = Y1_test
# Das LinearRegression-Modell wird erstellt
model3 = linear_model.LinearRegression()
# und mit den transformierte Featuren trainiert
model3.fit(X3_train, Y3_train)
# Die Genauigkeit wird berechnet
result = model3.score(X3_test, Y3_test)
print("Accuracy: %.2f%% (1 feature, polynomial model, degree %i)" % (result * 100.0, degree))
Accuracy: 80.66% (1 feature, polynomial model, degree 6)
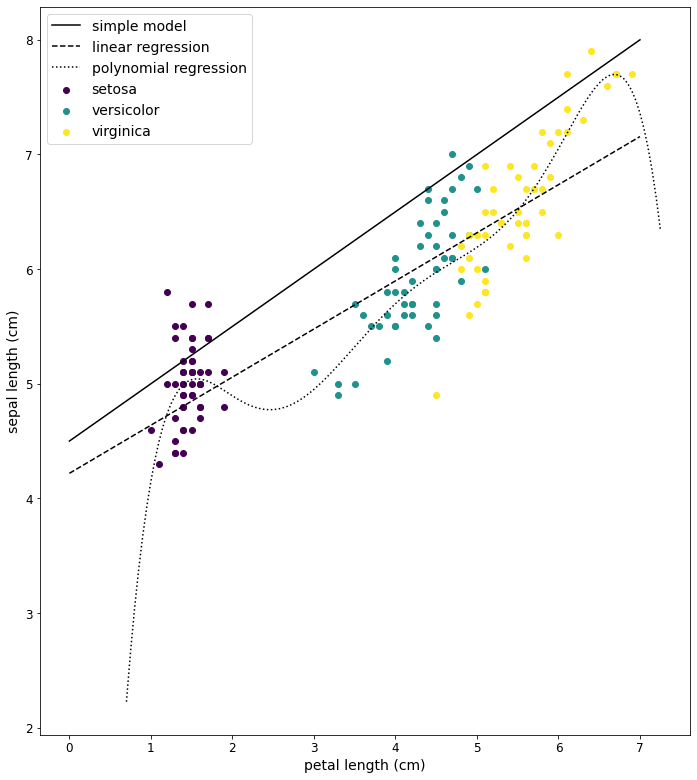
# Diagramm erstellen # - Features (setosa, versicolor, virginica) # - Vorhersage der einfachen Funktion (simple model) # - Vorhersage des LinearRegression-Modells # - Vorhersage mit Polynomial Regression import operator fig, axes = scatter_plot_2d(False, figsize=(10, 11)) Rl = np.array([0,7]) axes.plot(Rl, simple_model(Rl.reshape(-1,1)),color='k' , label="simple model") axes.plot(R, model1.predict(R.reshape(-1,1)),color='k',linestyle="--", label="linear regression") step = 0.05 Rp = np.arange(0.7, 7.3, step) Rp_poly = polynomial_features.fit_transform(Rp.reshape(-1, 1)) Y3_poly_pred = model3.predict(Rp_poly) sort_axis = operator.itemgetter(0) sorted_zip = sorted(zip(Rp, Y3_poly_pred), key=sort_axis) Xp_plot, Yp_plot = zip(*sorted_zip) axes.plot(Xp_plot, Yp_plot, color='k',linestyle=":", label="polynomial regression") axes.legend(fontsize=14) plt.show()
Die Genauigkeit (Accuracy) dieses Modells ist über 80% und damit ist es besser als die beiden anderen Modelle. Anhand des Diagramms ist hier gut zu erkennen, dass die Kurve bei sehr kleinen und sehr großen Werten für das Feature petal length sehr stark von den bekannten Werten für das Label sepal length abweicht.
Das Modell ist sehr gut für die bekannten Daten geeignet. Neue, bisher unbekannte Daten können aber zu einem sehr großen Fehler bei der Vorhersage führen. Dieses Verhalten wird auch Overfitting genannt.
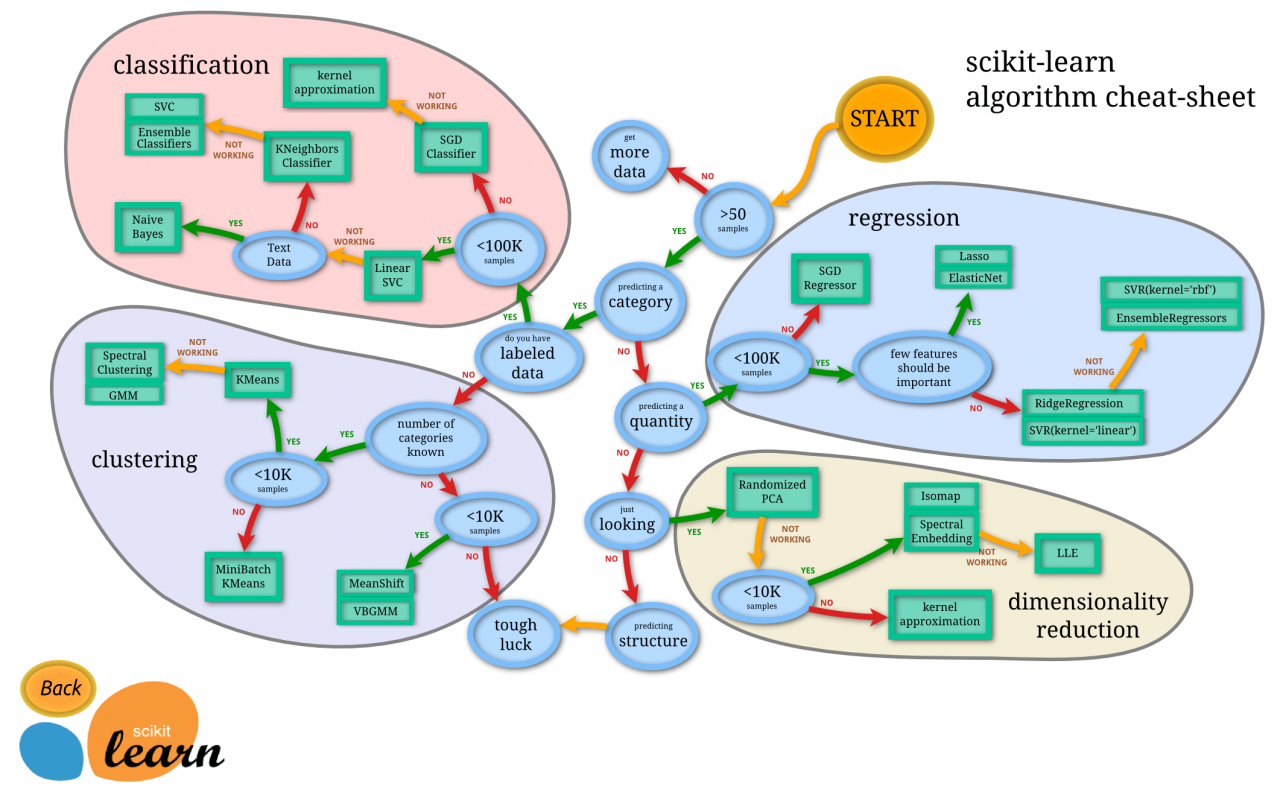
Scikit-Learn und andere Bibliotheken
Für Machine Learning gibt es viele unterschiedliche Anwendungsfälle und viele unterschiedliche Algorithmen. Die folgende Abbildung gibt einen Überblick über die verschiedenen scikit-learn Algorithmen.
Image(filename="scikit-learn-ml_map.png")
Neben scikit-learn gibt es noch viele weitere ML-Bibliotheken. Hier eine unvollständige Auflistung:
- TensorFlow
- XGBoost
- Spark MLlib
- PyTorch
Arten von Problemen
Wie in der Abbildung dargestellt, wird beim Machine Learning zwischen mehreren unterschiedlichen Problemstellungen unterschieden. Diese werden hier kurz vorgestellt.
Regression
Hier geht es um die Vorhersage von beliebigen reellen Werten. Die hier verwendeten Modelle zur Vorhersage der Länge des Kelchblattes (sepal length) sind Beispiele für Regressionsmodelle.
Klassifikation
Bei der Klassifikation geht es um die Vorhersage der Zugehörigkeit von unbekannten Daten zu bereits festgelegten Klassen. Die Vorhersage der Art (class) einer Schwertlilie ist ein typisches Klassifikationsproblem.
Clustering
Clustering-Algorithmen teilen die Daten in Gruppen (Cluster) ein. Im Gegensatz zur Klassifikation sind hier die Gruppen meistens nicht bekannt. Für das Iris Dataset kann ein Clustering-Modell anhand der Maße der Blätter die drei verschiedenen Arten erkennen und die Datensätze den einzelnen Gruppen zuordnen.
Dimensionsreduktion
Bei der Dimensions-Reduktion geht es darum, Zusammenhänge und Korrelationen der Features eines Datasets automatisch zu erkennen und die Anzahl der Features (Dimensionen) so zu reduzieren, dass die relevanten Informationen erhalten bleiben. Zum Beispiel könnte (bzw. sollte) ein solches Modell erkennen, dass von den beiden Features petal length (Länge des Kronblattes) und petal width (Breite des Kronblattes) nur eins benötigt wird.
Arten von Machine Learning
Beim Machine Learning wird grundsätzlich zwischen drei Arten unterschieden. Diese werden im Folgenden kurz erklärt.
Supervised Learning
Beim Supervised Learning werden zum Trainieren des Modells Eingabedaten (Features) und bekannte Ergebnisse (Label) verwendet. Die gezeigten Regressions-Modelle sind Beispiele für das Supervised Learning.
Unsupervised Learning
Beim Unsupervised Learning sind für die Trainingsdaten die erwarteten Ergebnisse (Label) nicht bekannt oder werden zum Trainieren nicht benötigt. Das Modell versucht, in den Trainingsdaten selbständig Muster zu erkennen. Unsupervised Learning wird oft für das Clustering und die Dimensionsreduktion eingesetzt.
Reinforcement Learning
Im Gegensatz zum Supervised und Unsupervised Learning wird das Modell beim Reinforcement Learning nicht mit einem umfangreichen Datensatz trainiert. Stattdessen lernt das Modell von der Interaktion mit seinem Umfeld. Über Feedback erfährt es, ob seine Entscheidungen gut oder schlecht waren und es passt sein Verhalten entsprechend an. Ein Beispiel dafür ist ein System, dass die Regeln für das Spiel Tic-Tac-Toe kennt und lernt, wie es spielen muss, damit es nicht verliert. Feedback ist in diesem Fall das Ergebnis des Spiels (gewonnen, verloren oder unentschieden).
Ist das jetzt alles?
Nein, es gibt noch viel mehr!
In diesem Artikel ging es darum, ein grobes Verständnis dafür zu schaffen, was Machine Learning ist und wie es funktioniert. Im Kern ist Machine Learning eine Kombination aus Mathematik und Informatik. Durch frei verfügbare Bibliotheken, wie zum Beispiel scikit-learn, wird der Einstieg deutlich vereinfacht. Insbesondere müssen die verschiedenen Algorithmen nicht selber implementiert werden.
Allerdings ist es auch sehr leicht, hier die Orientierung zu verlieren. Für einen guten Start empfehle ich unser Seminar "Einführung in Maschinelles Lernen". An drei Tagen werden hier die wichtigsten theoretischen Grundlagen vermittelt und in vielen praktischen Übungen direkt angewendet.
Für eine unabhängige Beratung zu Machine Learning und zu vielen anderen Themen, wie zum Beispiel Big Data, Cloud oder (NoSQL) Datenbanken, stehen Ihnen unsere erfahrenen Berater*innen gerne zur Verfügung.
Sie haben Interesse an einer Weiterbildung oder Fragen zum Thema Machine Learning? Sprechen Sie uns an oder besuchen Sie einen unserer Kurse aus unserem Seminarshop:
Zu unseren ML Seminaren



Kommentare